深度学习模型实现核聚变等离子体预测成本降低，精度提升至十万分之一，速度快近1000倍

编辑 | 2049

在聚变能源研究领域，等离子体动力学模拟发挥着至关重要的作用。然而，非线性Fokker-Planck-Landau（FPL）碰撞算子的计算成本极为高昂，尤其在全托卡马克体积建模中，其计算时间随着等离子体粒子种类数量n的增加呈O(n²)的增长，这严重限制了模拟的效率。

为了解决这一瓶颈，来自蔚山国立科学技术院（UNIST）的研究人员开发了一种全新的深度学习框架——FPL-net，旨在利用人工智能技术加速求解这一复杂问题。

FPL-net的结果获取速度是以往方法的1,000倍，且误差幅度仅为十万分之一，显示出其卓越的准确性。

该研究的论文题目为《FPL-net：解决各向异性温度放松的非线性Fokker-Planck-Landau碰撞算子的新型深度学习框架》，于2025年2月15日刊载在《Journal of Computational Physics》上。

论文链接：https://doi.org/10.1016/j.jcp.2024.113665

相关报道：https://phys.org/news/2025-02-deep-boosts-plasma-nuclear-fusion.html

研究背景

在托卡马克聚变设备中，非线性Fokker-Planck方程是描述等离子体碰撞过程的核心数学工具。传统上，该方程可以表示为Landau形式或Rosenbluth形式的积分微分方程，这两种形式均需复杂的数值方法进行求解。

尽管科研人员已开发出多种数值方法以确保质量、动量和能量的守恒，然而由于碰撞算子的非线性特性，其计算速度依然不及线性算子，因而成为等离子体模拟中的主要计算瓶颈。

FPL-net：革新的深度学习解决方案

FPL-net的核心构架是一个经过优化的全卷积神经网络，采用U-Net架构作为其支撑网络。

U-Net最初是为生物医学图像分割领域设计的，它由一个负责捕获输入图像上下文的编码器和一个负责实现精确定位和高分辨率输出的解码器组成。

该编码器-解码器架构能够保持输入与输出的尺寸一致，保留高分辨率的局部信息，同时在相对较小的模型规模下实现出色的性能。

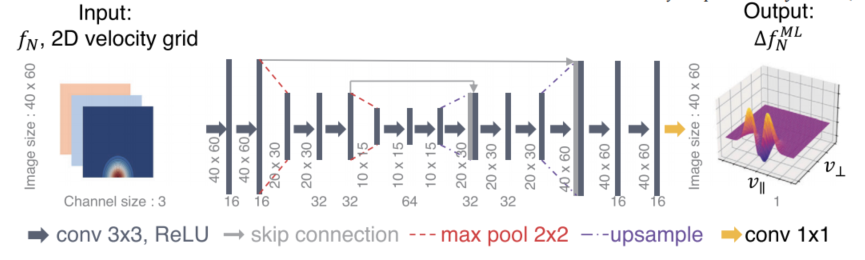
图示：以二维速度网格信息作为输入的任意概率分布函数（PDF）fN的FPL-net示意图。（来源：论文）

FPL方程可以表述如下：

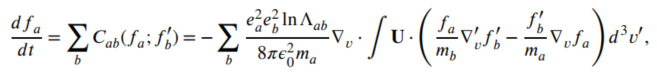
其中，a和b分别代表不同的粒子种类，f表示概率分布函数，C_ab为a与b之间的碰撞算子（在各自坐标系中为v和v’），e、m、ε₀和lnΛ分别是电荷、质量、真空介电常数和库仑对数。张量U定义为：

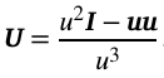
此处，u = v – v’为相对速度矢量，I为单位张量。

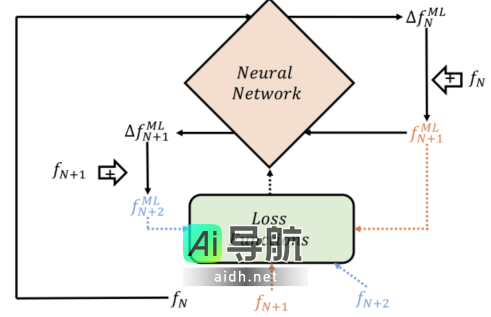
图示：训练过程的概述。（来源：论文）

研究团队利用传统的FPL求解器生成训练数据，采用有限体积法和Picard迭代方案，在二维速度网格上对电子等离子体进行模拟，网格尺寸为垂直轴（N⊥）和平行轴（N∥）均为N⊥×N∥=40×60。

为确保模型的泛化能力，研究人员准备了115种不同的各向异性初始温度条件的数据，平行轴温度（T∥）与垂直轴温度（T⊥）的比值范围在0.71到2.19之间，密度稳定为ne = 1.0×10¹⁹/m³，并设定垂直温度T⊥为100 eV。每个时间步长设置为碰撞时间的十分之一，在每种条件下进行了200个时间步长的模拟。

FPL-net的输入形式为一个三通道张量，由任意初始条件下的分布函数fN和二维速度网格（v⊥和v∥）组成，尺寸为40×60×3。通过堆叠分布函数和速度网格，模型得以学习与分布函数相关的速度几何信息，从而保持动量与能量的守恒。

模型的输出为库仑碰撞引发的分布函数变化ΔfML_N，这是一个尺寸为40×60的单通道张量。通过将输入fN与输出ΔfML_N相加，可以预测下一时间步的分布函数fML_N+1。

物理守恒约束与训练过程

FPL-net的独特之处在于其对物理守恒定律的处理。研究团队基于动力学理论中的分布函数矩，实现了物理守恒的约束：

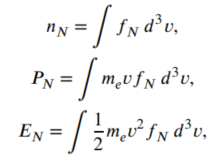
依托这些定义，团队构建了三个守恒损失函数：

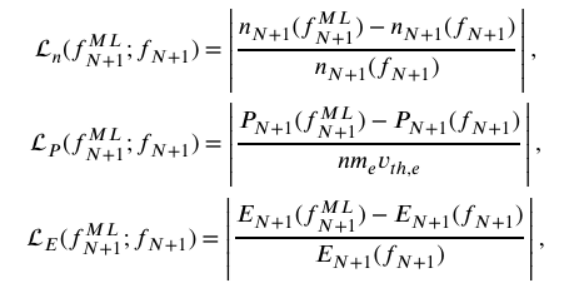
总体物理信息损失函数为：

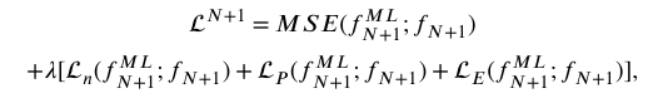
其中λ为可变超参数，代表守恒损失在总损失函数中的权重，初始值设定为0，并在600个epoch的过程中线性增加到0.5，之后保持不变。

图示：模型评估过程的流程图。FPL-net 在维持误差控制在 10⁻⁵ 量级的同时，展现了卓越的计算效率。在针对测试数据集的 2189 个测试案例中，密度误差的平均值为 9.82×10⁻⁶，中位数为 7.81×10⁻⁶；动量误差的平均值则为 5.46×10⁻⁶，中位数为 4.27×10⁻⁶；能量误差的平均值为 2.85×10⁻⁵，中位数为 2.13×10⁻⁵。

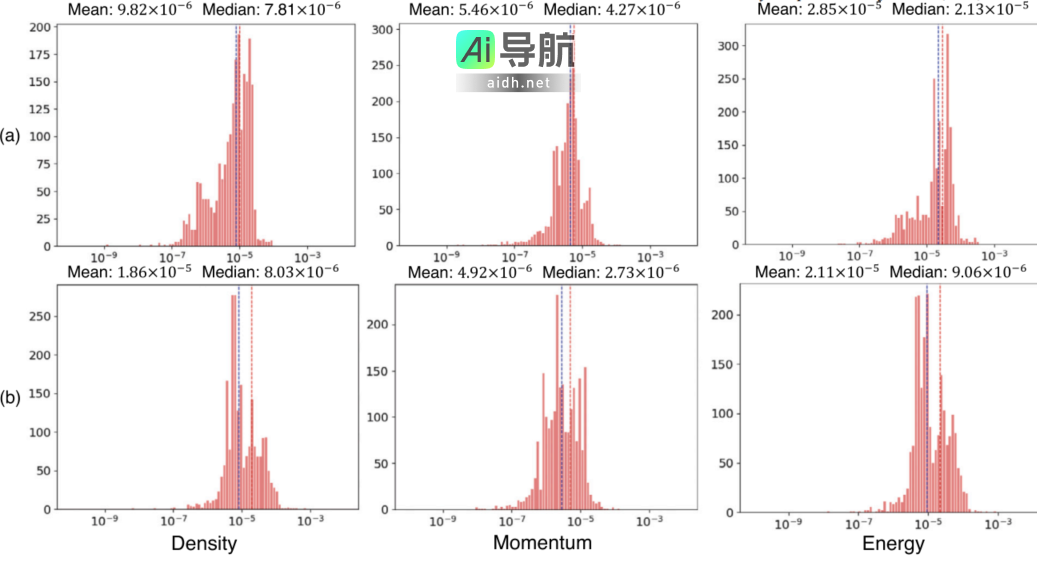
图示：基于 2189 个测试用例的密度（左）、动量（中）和能量（右）误差分布的直方图。（来源：论文）

FPL-net 成功实现了完整的温度松弛，这是深度学习模型在该领域首次取得的重大突破。在以初始条件 T∥/T⊥=0.795 进行的温度松弛实验中，与基于 Picard 迭代碰撞代码所获得的真实数据相比，双麦克斯韦松弛过程展现出显著的一致性，在 199 个时间步内，最大差异仅为 3.3%。

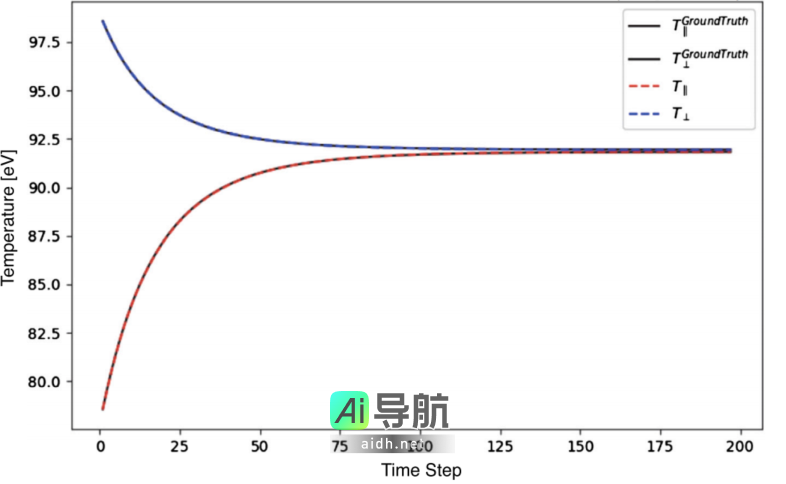
图示：在初始温度条件 T∥/T⊥ = 0.795 下，温度弛豫实验在 199 个时间步长中的结果。黑色实线表示真实数据，红色（蓝色）虚线表示从 FPL-net 结果推导出的 v∥（v⊥） 温度。（来源：论文）

研究团队还进行了两项额外的实验，以验证模型的稳健性。

在延长推演测试中，模型的预测长度扩展至 1200 个时间步（相较于训练长度的六倍），结果表明在 1000 个时间步内的误差保持在可接受范围，温度与真实值非常契合。

在进行高斯噪声测试时，向输入添加的噪声分别为输入标准差的 1%、2.5% 和 5%，结果显示，在噪声水平不超过 2.5% 的情况下，误差不会随时间步的增加而发散，温度松弛得以成功实现。

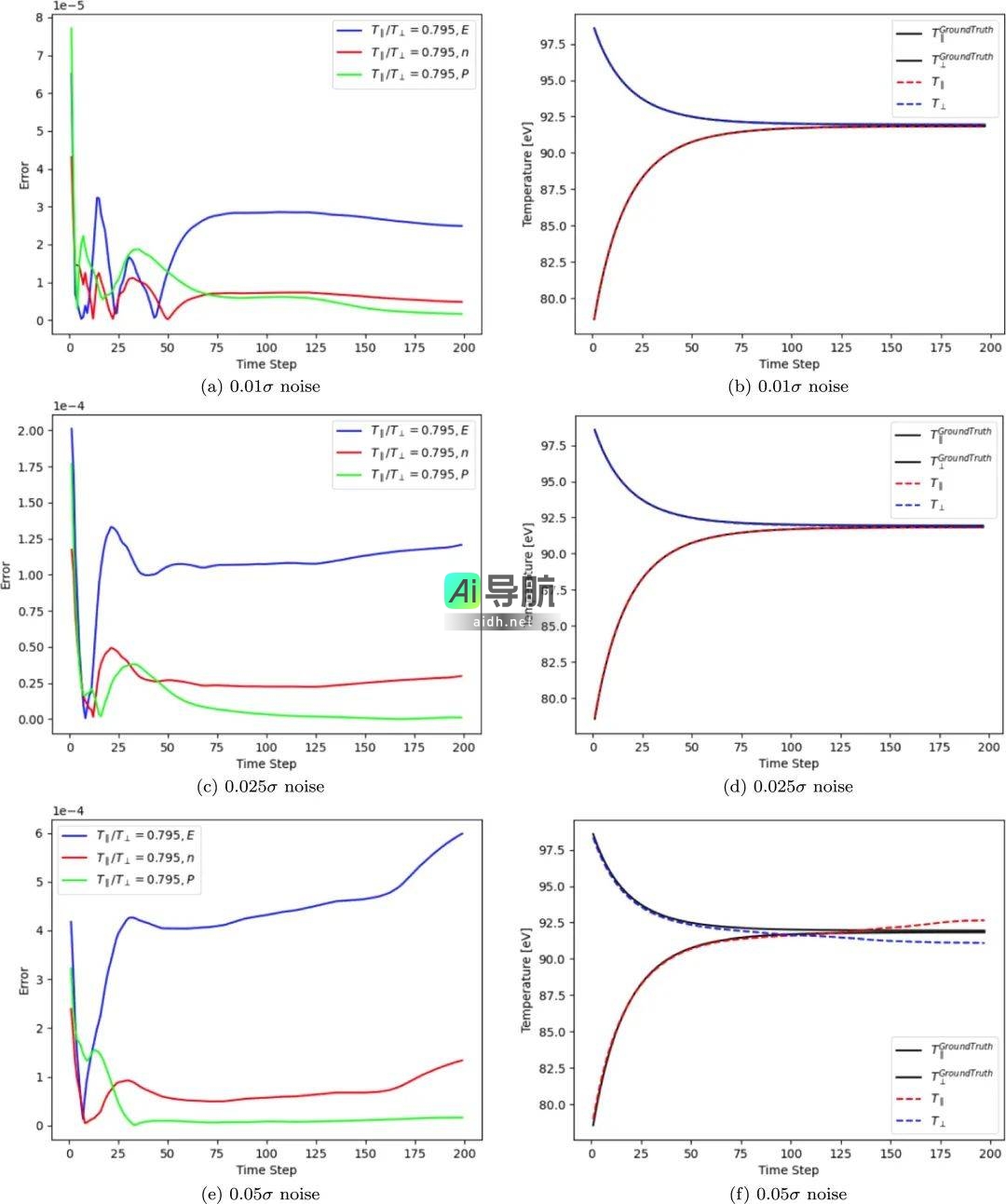
图示：应用随机噪声的 FPL-net 预测结果。（来源：论文）

在计算效率方面，FPL-net 在单个 NVIDIA RTX A5000 GPU 上，每个时间步的平均推理时间为 3.56 毫秒，内存占用为 63.82 MB。

相比之下，Picard 迭代碰撞算子在 Intel Xeon Silver 4112 CPU 上每个时间步平均需要 4135 毫秒，并消耗 1017 MB 的内存。

这表明，FPL-net 与传统数值方法相比，实现了超过 1000 倍的加速。

未来展望与挑战

作为深度学习在等离子体碰撞模拟应用的典范，FPL-net 证明了在维持高精度的同时显著降低计算成本的可行性。这一计算加速让研究人员能够更高效地利用有限的资源，加快等离子体研究进程，并为数字孪生托卡马克及全装置建模提供了必要支持。

然而，该研究依然存在明显的局限性：当前 FPL-net 仅能模拟电子等离子体，且不包括主要离子，初始分布函数也仅限于双麦克斯韦分布。未来的研究将致力于开发包含多种粒子的碰撞算子，扩展至更广泛的初始分布函数，以提升其在聚变领域的实际应用价值。